Why? Never heard of a hotel, or airplane camping? If you're retired, or took a month off, why do you have to return home after every couple airports?
A number of years ago I took a Data Structures and Algorithms class in Java. One of the assignments was the Traveling Salesman problem. Later, I decided I wanted something similar, but in Python, for optimizing my flight simulation goal of flying to every airport in the world. I quickly discovered that it was O(N!). I optimized it a bit. As the trial path was computed, as soon as it was longer than the shortest path so far, that trial was terminated. Also, I made it open jaw, so the start and finish airports could be different. That way, I could enter a block of airports on one side, optimally visit the airports in that group, and finish close to the next group of airports. Thus, the runtime would be M*O(N!) instead of O((M*N)!) Where M is the number of airport groups, and N is the number of airports in the group. My version of Python is single threaded. If I rewrite the program, it will be in C++, which supports multi-threading. That should speed things up, but probably not by the number of threads supported. I also wrote a program that converts differences in Lat/Long into distances. Crossing the International Date line requires some care, but as far as I could tell, I did it correctly. I never could get the bearing calculations to work correctly, but FSX:SE's flight planner gave the correct bearings.
If doing it as a round robin you don't have to do n! calcs. On a clock the shortest distance around is never going to be 1 7 2 8 3 9 4 10 5 11 6 12 1.
As much as I like working out the math, someone already did it for us in the Aviation Formulary. https://edwilliams.org/avform.htm
Because MOST people are not retired, can't take off a month, and wouldn't spend the money for the hotels. But then you would have to add in the factor of airports with close by hotels and possibly courtesy cars to end up at the end of each day. And deal with how many airports you can do each day.
I don't have maps, but I do have a script in R that can solve the TSP problem (within less than or equal to twice the optimal length of the tour). With a bit more effort (maybe I'll come back to it later), one could extend this to produce some maps/graphics. You can download the dataset that this script uses from OurAirports dot com. You can download R and Rstudio from CRAN and Posit, respectively, to execute the script. There are R online interpreters, but most likely they won't let you install the packages you need to run this script. You can lookup the theory behind the heurstic algorithms by reading the vignette for the TSP package on CRAN (just search CRAN TSP, click on the link, halfway down that ugly text page will be a thing called "vignette" that you can click on that will open a PDF that explains all the math and such). Feel free to customize the filter to pick which airports you want to find the best route for. Calculating the distance matrix has quadratic space complexity, so you can eat up hundreds of gigabytes of RAM pretty quickly if you have more than say 10,000 airports in the list (I ran out of memory trying to do all airports in the U.S. anyways, and I have 64 Gigs; there are probably more efficient implementations for calculating the distance matrix, though they may not be compatible with the TSP package). Memory usage also scales based on the number of CPU cores you throw at the problem (each core has to have a copy of the data). By the way, the code will max out your CPU if you let it, so feel free to reduce the number of iterations (which may reduce how optimal the result is) or the number of CPUs to match your machine. 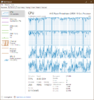I can't post links yet, so below are screenshots, followed by the pasting of the code. In this example, I calculated the route of all open airports, balloonports, and heliports in Arkansas which have a GPS code (per the data source). # install.packages(c("TSP", "dplyr", "data.table", "geosphere", "doParallel")) library(TSP) library(dplyr) library(data.table) library(geosphere) library(doParallel) iterations <- 100 numCores <- 16 registerDoParallel(cl = numCores) airports <- fread("I'm not allowed to post links yet") desired_airports <- airports %>% filter(type != "closed", iso_country == "US", iso_region == "US-AR", ident != "", gps_code != "") distance_matrix <- as.matrix(distm(desired_airports %>% select(longitude_deg, latitude_deg))) / 1000 # convert meters to kilometers rownames(distance_matrix) <- desired_airports$ident colnames(distance_matrix) <- desired_airports$ident methods <- c("nearest_insertion", "cheapest_insertion", "farthest_insertion", "arbitrary_insertion", "nn", "repetitive_nn", "two_opt") distTSP <- as.TSP(distance_matrix) solutions <- lapply(methods, function(m) solve_TSP(distTSP, method = m, two_opt = T, rep = numCores*iterations)) stopImplicitCluster() tour_lengths <- sapply(solutions, tour_length) best_solution <- solutions[[which(tour_lengths == min(tour_lengths))]] print(best_solution) best_airport_route <- labels(best_solution)
There might be a Python package out there that can do this (python-tsp, for example)! The nice thing about R is that you can call Python code from within it using the reticulate package (and you can send R objects to Python, do computations on it, and then pull Python objects back into R, and do computations on that, all within a single script, pretty seamlessly). I don't know if there is an equivalent to the reticulate package in Python, though (which one would think is possible since the package exists for inter-operability). In this case, the R package geosphere and TSP are doing all the hard work (for calculating the distance matrix from lat/long points and solving the TSP problem, respectively), and those packages may have underlying implementations in C++, RCpp, and/or Fortran.
Edit: The below code assumes Euclidean distance, which does not scale well when the curvature of the Earth becomes a significant factor. The code above does not have this problem (it calculates distance on the ellipsoid WGS84, which is the best global ellipsoid overall at present per the documentation (but not the optimal in all places of the Earth)). It turns out it is fairly easy to modify my earlier script to produce a plot. Still doesn't have several features I would like to see, such as labels on the points, a map of the world behind it, or is interactive so you can zoom in and out, but I'm sure it's all solvable (probably with ggplot2 or as a Shiny app). Here are two such plots (remember, the heuristics have random components). Coordinates are latitude and longitude for y and x, respectively. Updated code is below. Code: library(TSP) library(dplyr) library(data.table) library(geosphere) library(doParallel) numCores <- 8 iterations <- numCores * 200 registerDoParallel(cl = numCores) airports <- fread("https://davidmegginson.github.io/ourairports-data/airports.csv") desired_airports <- airports %>% filter(type != "closed", iso_country == "US", iso_region == "US-AR", ident != "", gps_code != "", gps_code != "5AK4") # airport misclassified, should be in US-AK etsp <- as.ETSP(data.frame(x = desired_airports$longitude_deg, y = desired_airports$latitude_deg, row.names = desired_airports$gps_code)) #distance_matrix <- as.matrix(distm(desired_airports %>% select(longitude_deg, latitude_deg))) / 1000 # convert meters to kilometers #rownames(distance_matrix) <- desired_airports$gps_code #colnames(distance_matrix) <- desired_airports$gps_code methods <- c("nearest_insertion", "cheapest_insertion", "farthest_insertion", "arbitrary_insertion", "nn", "repetitive_nn", "two_opt") #distTSP <- as.TSP(distance_matrix) #solutions <- lapply(methods, function(m) solve_TSP(distTSP, method = m, two_opt = T, rep = iterations)) solutions <- lapply(methods, function(m) solve_TSP(etsp, method = m, two_opt = T, rep = iterations)) stopImplicitCluster() tour_lengths <- sapply(solutions, tour_length) best_solution <- solutions[[which(tour_lengths == min(tour_lengths))]] print(best_solution) best_airport_route <- labels(best_solution) print(best_airport_route) plot(etsp, best_solution, tour_col = "red")
Java: https://www.javatpoint.com/travelling-salesman-problem-in-java Python & C++ https://www.guru99.com/travelling-salesman-problem.html
In the '90s, I heard that there was a guy who embarked on a project to fly 40 instrument approaches on his 40th birthday. I bet he was real tired when he got done with that!
True, but who would/could take the time to hit 100 airports in one long trip? MD is only 33, so not too bad.
I used to fly out of there for helicopter training. It was a nice airport. I hear, later it was worse than Laurel.
I've done 6 in about 90 minutes without dropping the gear and flying at cruise speed. Runway heading lines me up with next IAF, so I'm being pretty efficient. Can't imagine do that 6 more times.
I was based at VKX for years prior to 9/11. W32 was pretty decrepit then. They had to mow the (paved) runway to keep the weeds at bay. Not much in the way of services. The only thing that kept it alive toward the end was Stan Fetter who operated is traffic reporting business out of there.
10 public use airports in reality. Even Rhode Island has 7. N06 - Laurel IGL - New Castle GED - Delaware Coastal EVY - Summit D74 - Chorman 38N - Smyrna 33N - Delaware Airpark 15N - Jenkins 0N6 - Albanna Aviation 0N4 - Chandelle The smallest - Chandelle is just 2500 x 28'...I try to avoid runways narrower than my wingspan.
Yep, all 10. Touch and go on some, full stop taxi back on others. Chandelle stands out because it has (or had) a tree right off the departure end on centerline. I think Jenkins was the "roughest", just a little grass runway with what looked like aircraft in various stages of decay and salvage along the sides. Like an airplane graveyard. It's been 18 years but some things still stand out!
Used to be one on Kent Island that the runway about 1 foot wider than the landing gear of the 172 I landed there.
So, while my code produces a route and doesn't really graph it, SkyVector can give you a graph pretty easily once you have a list of airport IDs. You can take the output of my code, select the gps_code column, and print it with each code on a newline (solution %>% select(gps_code) %>% pull %>% cat(sep="\n")), then paste that into SkyVector's flightplan and hit Enter. For example, a route of all open airports in Texas which have scheduled service or are large or or are medium and either have a homepage or Wikipedia link, is shown below. (Note that I solved all Texas airports and then filtered to this list, and a subset of a solution of a Traveling Salesman Problem is not guaranteed to be optimal due to the multi-dimensionality of the problem, not to mention my code uses a heuristic so it can work at scale so the solution isn't optimal to begin with, so there's some weird behavior in this example routing).
