alfadog
Final Approach
That video gave me the feels...
I can see how it might. I had no idea that you could "tune" a square like that. I like that a lot. I do know the analogous way to check a level.
That video gave me the feels...
Chicken, or egg?The idea is to get the students interested in and invested in STEM, which is an area that we are falling behind in. Not just give them a formula to cut a board. Or we could just keep giving our best jobs to highly-educated immigrants under H-1B visas and the like (assuming for the moment that this video is of a US classroom).
https://www.engineeringforkids.com/about/news/2016/february/why-is-stem-education-so-important-/
"According to the U. S. Department of Commerce, STEM occupations are growing at 17%, while other occupations are growing at 9.8%. STEM degree holders have a higher income even in non-STEM careers. Science, technology, engineering and mathematics workers play a key role in the sustained growth and stability of the U.S. economy, and are a critical component to helping the U.S. win the future. STEM education creates critical thinkers, increases science literacy, and enables the next generation of innovators. Innovation leads to new products and processes that sustain our economy. This innovation and science literacy depends on a solid knowledge base in the STEM areas. It is clear that most jobs of the future will require a basic understanding of math and science. Despite these compelling facts, mathematics and science scores on average among U.S. students are lagging behind other developing countries." Emphasis added, LOL
There's a simpler demonstration:
Works for all right triangles.
Your image does not prove that c^2 = a^2 + b^2. What he offered was a graphical proof. I don't remember how the proof of the theorem was presented to me way back when but that seemed brand new to me in that I do not think I have seen it before.
I have no problem with the way the information was presented, nor the impact that a great teacher has on maintaining the interest of his students (especially in STEM fields). My point was that I feel like I was missing some "connection" that was to be made with the example. I was hoping someone might expound on why the example of relating the area of the empty space and the area of the right triangles was critical to the theorem itself, or if it was just an illustration on how to use a2xb2=c2 to solve a slightly more difficult scenario.
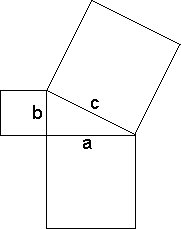
This was the image which I was more familiar with: which shows that a square with 4-equilateral sides of "a", and a square with 4-equilateral sides of "b", then the sum of those equals a square with 4-equilateral sides of "c".
Absolutely a proof. In fact it's the one most commonly attributed to Pythagoras himself.
Here is it in 5 seconds, which may make it seem more familiar (probably won't play/animate on a phone):
https://upload.wikimedia.org/wikipedia/commons/9/9e/Pythagoras-proof-anim.svg
THAT IS MY POINT! The image I provided was an application (or representation) of the theorem which shows how the area of a square attached to each side of a right triangle would have areas consistent with the theorem formula. What I don't understand, is how the teacher's example is a "proof" of that theorem as opposed to another example of an application of the theorem. Hence why I said I feel like I'm missing the connection.
I have no problem with the way the information was presented, nor the impact that a great teacher has on maintaining the interest of his students (especially in STEM fields). My point was that I feel like I was missing some "connection" that was to be made with the example. I was hoping someone might expound on why the example of relating the area of the empty space and the area of the right triangles was critical to the theorem itself, or if it was just an illustration on how to use a2xb2=c2 to solve a slightly more difficult scenario.
This was the image which I was more familiar with: which shows that a square with 4-equilateral sides of "a", and a square with 4-equilateral sides of "b", then the sum of those equals a square with 4-equilateral sides of "c".

But yours is not a proof. It is a representation of the formula. You go into it knowing the lengths of all sides.
It is absolutely a proof. Graphical representations can be proofs. Do it with unknown sides, then.
Your graphic has no meaning with unknown sides. That is why it is not a proof. The fellow in the video does a graphical representation as a proof.
It absolutely does.
[Delete random insults and silliness]
Just because I labeled the sides in the example to help people out doesn't negate the proof.
There are over 300 different proofs of the theorem and the one I showed is one of the accepted ones.You continue to confuse a demonstration with a proof. I don't think that's going to change by virtue of anything I say here.
